Given data:
The first side of the triangle is p=13 inches.
The second side of the triangle is q=18 inches.
The third side of the triangle is r= 12 inches.
The semi-perimeter is,
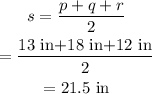
The expression for the area of the triangle is,
![\begin{gathered} A=\sqrt[]{s(s-p)(s-q)(s-r)_{}} \\ =\sqrt[]{21.5\text{ in(21.5 in-13 in)(21.5 in-18 in)(21.5 in-12 in)}} \\ =\sqrt[]{(21.5\text{ in)(8.5 in)(3.5 in)(9.5 in)}} \\ =77.95in^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/th75b70stki08vcs910f3flptlaidzyyzh.png)
Thus, the area of the given triangle is 77.95 sq-inches.