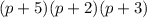Question

Find the lowest common denominator of - not graded !

Answer 1

Given:

There are two equation given in the question.

Required:

We have to find the lowest common denominator of both equation.

Step-by-step explanation:

`(p+3)/(p^2+7p+10)and(p+5)/(p^2+5p+6)`

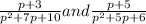
are given equations

first of all we need to factorization both denominator

`\begin{gathered} p^2+7p+10and\text{ }p^2+5p+6 \\ (p+5)(p+2)and\text{ \lparen p+3\rparen\lparen p+2\rparen} \end{gathered}`

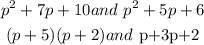
so here (p+2) is common in both so take (p+2) for one time only

so now the lowest common denominator is

`(p+5)(p+2)(p+3)`

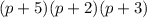
Final answer:

The lowest common denominator for given two equations is

`(p+5)(p+2)(p+3)`