Question

create an original function that has at least one asymptote and possibly a removable discontinuity list these features of your function: asymptote(s) (vertical horizontal slant) removable discontinuity(ies) x intercept(s) y intercept and end behavior provide any other details that would enable another student to graph and determine the equation for your function do not state your function

Answer 1

We have to create a function that has at least one asymptote and one removable discontinuity (a "hole").

We then have to list the type of feature.

We can start with a function like y = 1/x. This function will have a vertical asymptote at x = 0 and a horizontal asymptote at y = 0.

We can translate it one unit up and one unit to the right and write the equation as:

`y=(1)/(x-1)+1=(1)/(x-1)+(x-1)/(x-1)=(x)/(x-1)`

Then, the asymptotes will be x = 1 and y = 1. We have at least one asymptote for this function.

We can now add a removable discontinuity. This type of discontinuity is one that is present in the original equation but, when factorizing numerator and denominator, it can be cancelled. This happens when both the numerator and denominator have a common root: the rational function can be simplified, but the root is still present in the original expression.

We than can add a removable discontinuity to the expression by multiplying both the numerator and denominator by a common factor, like (x-2). This will add a removable discontinuity at x = 2.

We can do it as:

`y=(x(x-2))/((x-1)(x-2))=(x^2-2x)/(x^2-3x+2)`

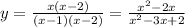
This will have the same shape as y =x/(x-1) but with a hole at x = 2, as the function can not take a value that makes the denominator become 0, so it is not defined for x = 2.

Finally, we can find the x and y intercepts.

The y-intercepts happens when x = 0, so we can calculate it as:

`\begin{gathered} f(x)=(x^2-2x)/(x^2-3x+2) \\ f(0)=(0^2-2\cdot0)/(0^2-3\cdot0+2)=(0)/(2)=0 \end{gathered}`

The y-intercept is y = 0, with the function passing through the point (0,0).

As the x-intercept is the value of x when y = 0, we already know that the x-intercept is x = 0, as the function pass through (0,0).

Then, we can list the features as:

Asymptotes: Vertical asymptote at x = 1 and horizontal asymptote at y = 1.

Removable discontinuity: x = 2.

y-intercept: y = 0.

End behaviour: the function tends to y = 1 when x approaches infinity or minus infinity.

With that information, the function can be graphed.