Question

Use the given conditions to write an equation for the line.Passing through (−7,6) and parallel to the line whose equation is 2x-5y-8=0

Answer 1

`y\text{ = }(2)/(5)x\text{ + }(44)/(5)`

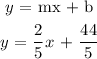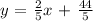
Step-by-step explanation:

For a line to be parallel to another line, the slope will be the same

1st equation:

`\begin{gathered} 2x\text{ - 5y - 8 = 0} \\ \text{making y the subject of formula:} \\ 2x\text{ - 8 = 5y} \\ y\text{ = }\frac{2x\text{ - 8}}{5} \\ y\text{ = }(2x)/(5)\text{ - }(8)/(5) \end{gathered}`
`\begin{gathered} \text{equation of line:} \\ y\text{ = mx + b} \\ m\text{ = slope, b = y-intercept} \end{gathered}`
`\begin{gathered} \text{comparing the given equation and equation of line:} \\ y\text{ = y} \\ m\text{ = 2/5} \\ b\text{ = -8/5} \end{gathered}`

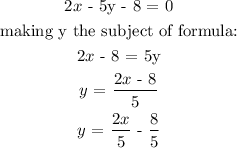
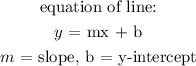
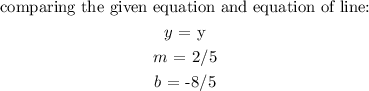
Since the slope of the first line = 2/5, the slope of the second line will also be 2/5

We would insert the slope and the given point into equation of line to get y-intercept of the second line:

`\begin{gathered} \text{given point: (-7, 6) = (x, y)} \\ y\text{ = mx + b} \\ 6\text{ = }(2)/(5)(-7)\text{ + b} \\ 6\text{ = }(-14)/(5)\text{ + b} \\ 6\text{ + }(14)/(5)\text{ = b} \\ \frac{6(5)\text{ + 14}}{5}\text{ = b} \\ b\text{ = }(44)/(5) \end{gathered}`

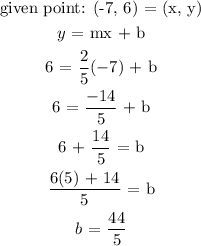
The equation for the line that passes through (-7, 6) and parallel to line 2x - 5y - 8 = 0:

`\begin{gathered} y\text{ = mx + b} \\ y\text{ = }(2)/(5)x\text{ + }(44)/(5) \end{gathered}`