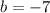Answer:
The y-intercept b for the derived equation is;
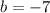
Step-by-step explanation:
Given that the line passes through the point (4,-9) and has a slope of -1/2;
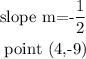
Applying the point-slope form of linear equation;

substituting the slope and the given point;
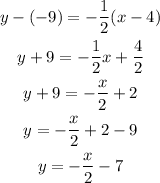
Comparing it to the slope intercept form of linear equation;

where;
m = slope
and b = y-intercept
Therefore, the y-intercept b for the derived equation is;