Question

Explain when you can cancel a number that is in both the numerator and denominator and when you cannot cancel out numbers that appear in both the numerator and the denominator.

Answer 1

Let me write here an example of a common number/term in both numerator and denominator that we can cancel.

`(4xy)/(4)=xy`

In the above example, we are able to cancel out the common number 4 because they are stand alone numbers. We can divide 4 by 4 and that is 1. Hence, the answer is just xy.

Another example:

`((x+2)(x-1))/((x+2)(2x-1))=((x-1))/((2x-1))`

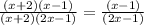
In the above example, we are able to cancel out (x + 2) because this term is a common factor to both numerator and denominator.

In the example, we can also see that -1 is a common number however, we cannot cancel it out because the number -1 is not a standalone factor. It is paired with other number/variable. (x - 1) and (2x - 1) are both factors but are not the same, that is why, we are not able to cancel that.

Another example:

`((x+2)+(x-1))/((x+2)+(2x-1))=((x+2)+(x-1))/((x+2)+(2x-1))`

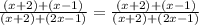
As we can see above, (x + 2) is a common term however, we cannot cancel it. We can only cancel common terms if they are common factors of both numerator and denominator. (Notice the plus sign in the middle. )

The term (x + 2) above is not a factor of the numerator and denominator, hence, we cannot cancel it.