Question

Kala the trainer had two solo workout plans that she offers her clients. PlanA and plan B. Each client does either one or the other (not both) on Friday there were 3 clients who did plan A and 5 who did plan B. On Saturday there were 9 clients who did plan A and 7 who did plan B. Kala trained her Friday clients for a total of 6 hours and her Saturday clients for a total of 12 hours. How long does each of the workout plans last?

Answer 1

Each of the workouts plans lasts 45 minutes.

Step-by-step explanation:

Let the duration for Plan A workout = x

Let the duration for Plan B workout = y

Friday

• Plan A --> 3 clients

,

• Plan B --> 5 clients

,

• Kala trained her Friday clients for a total of 6 hours

`3x+5y=6`

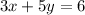
Saturday

• Plan A --> 9 clients

,

• Plan B --> 7 clients

,

• Kala trained her Saturday clients for a total of 12 hours

`9x+7y=12`

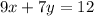
The system of equations is solved simultaneously.

`\begin{gathered} 3x+5y=6\cdots(1) \\ 9x+7y=12\cdots(2) \end{gathered}`

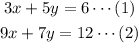
Multiply equation (1) by 3 in order to eliminate x.

`\begin{gathered} 9x+15y=18\cdots(1a) \\ 9x+7y=12\cdots(2) \end{gathered}`

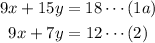
Subtract.

`\begin{gathered} 8y=6 \\ y=(6)/(8)=0.75\text{ hours} \\ 0.75*60=45\text{ minutes} \end{gathered}`

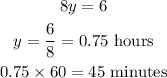
Substitute y=0.75 into equation (2) to solve for x.

`\begin{gathered} 9x+7y=12 \\ 9x+7(0.75)=12 \\ 9x+5.25=12 \\ 9x=12-5.25=6.75 \\ x=(6.75)/(9) \\ x=0.75 \end{gathered}`

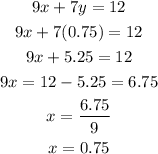
x=y=0.75 hours = 45 minutes,

Each of the workouts plans lasts 45 minutes.