Step-by-step explanation
To solve the question,
Let
The numerator = x
The denominator = y
So that the original equation will be
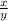
Next, we are told that the numerator is five times the denominator.
So that
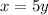
Again, we are told that If nine is added to both the numerator and the denominator, the resulting fraction is equivalent to two. so
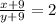
Hence
we can substitute x =5y into the above
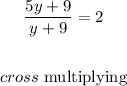
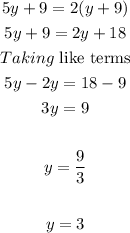
Thus, the denominator is 3
The numerator will be

The numerator is 15
Therefore, the fraction is
![undefined]()