A)
1 sample t-test
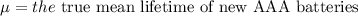
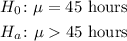

B)
Calculating t test statistic
![\begin{gathered} t=\frac{statistic-parameter}{s\tan dard\text{ deviation of statistic}} \\ t=\frac{\bar{x}-\mu_0}{\frac{s_x}{\sqrt[]{n}}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jn7jghq428ce6op16u2xm18mzvto07wvv7.png)
Plugging in the values, we have:
![\begin{gathered} t=\frac{\bar{x}-\mu_0}{\frac{s_x}{\sqrt[]{n}}} \\ t=\frac{46.9-45}{\frac{4.6}{\sqrt[]{50}}} \\ t=(1.9)/(0.6505) \\ t=2.9207 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y2k9zkcgorbz5tua5x74fvsxr6t8e0ezr5.png)
C)
t test statistic = 2.9207
degrees of freedom = n - 1 = 50 - 1 = 49
Using a calculator, we can calculate the p-value.
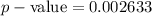
D)
Since p value is less than significance level (p value < alpha), then we will reject H_0 and take the alternate hypothesis.
Thus the test suggests that the new batteries do last more than 45 hours.
E)
We could've done Type I error here.
Type I error or α: Reject the null when it’s true.