Question

Find the probability and odds of winning the two-number bet (split) in roulette. Then find expected value of a $1 bet in roulette for the two-number bet.P.S Might not have enough information

Answer 1

We have to find the probaiblity of winning a split bet in roulette.

Then, we will have 2 numbers that will make us wind the bet out of 37 numbers that make the sample space.

We can then calculate the probability of winning the split bet as the quotient between the number of success outcomes (2) and the number of possible otucomes (37):

`P(w)=(2)/(37)\approx0.054`

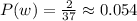
We can transform this into the odds of winning by taking into account that if 2 are the success outcomes, then 37-2 = 35 are the failure outcomes.

Then, the odds of winning are 2:35.

We now have to calculate the expected value for a $1 bet.

We know the probabilities of winning and losing, but we don't know the value or prize for winning.

The payout for a split bet is 17:1, meaning that winning a split bet of $1 has a prize of $17.

Then, we can use this to calculate the expected value as:

`\begin{gathered} E(x)=P(w)*w+P(l)*l \\ E(x)=(2)/(37)*17+(35)/(37)*0 \\ E(x)=(34)/(37) \\ E(x)\approx0.9189 \end{gathered}`

This means that is expected to win $0.9189 per $1 split bet.

Answer:

Probability of winning: 2/37 ≈ 0.054

Odds of winning: 2:35

Expected value of $1 split bet (17:1 payout): $0.9189