Question

The discriminant equation How many real solution 4x^2-8x+10=-x^2-5 have?

Answer 1

0 real solutions

Step-by-step explanation:

First, we need to transform the equation into the form:

`ax^2+bx+c=0`

So, the initial equation is equivalent to:

`\begin{gathered} 4x^2-8x+10=-x^2-5 \\ 4x^2-8x+10+x^2+5=-x^2-5+x^2+5 \\ 5x^2-8x+15=0 \end{gathered}`

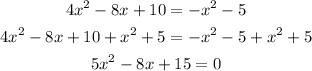
Now, the discriminant can be calculated as:

`b^2-4ac`

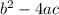
If the discriminant is greater than 0, the equation has 2 real solutions.

If the discriminant is equal to 0, the equation has 1 real solution

If the discriminant is less than 0, the equation has 0 real solutions

So, in this case, a is 5, b is -8 and c is 15. Then, the discriminant is equal to:

`(-8)^2-4\cdot5\cdot15=84-300=-236`

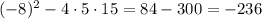
Since the discriminant is less than zero, the equation has 0 real solutions