Sample mean = 3.43
sample standard deviation = 2.07
Step-by-step explanation:
Given: 2, 3, 2, 5, 7, 1, 4
Total numbers = 7
1) Sample mean is calculated by finding the average of the data set
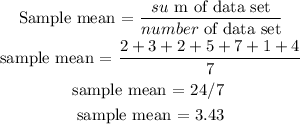
2) We have sample standard deviation and population standard deviation.
SInce the question asked for sample mean, we will be calculating sample standard deviation.
Standard deviation is calculated as:
![\begin{gathered} s\tan dard\text{ deviation = }\sqrt[]{\frac{\sum^{}_{}(x_1-mean)^2}{N-1}} \\ \\ s\tan dard\text{ deviation = }\sqrt[]{\frac{\sum ^{}_{}(2-3.43)^2+(3-3.43)^2+(2-3.43)^2+(5-3.43)^2+(7-3.43)^2+(1-3.43)^2+\mleft(4-3.43\mright)^2}{7-1}} \\ s\tan dard\text{ deviation = }\sqrt[]{(25.7143)/(6)}\text{ = }\sqrt[]{4.2857} \\ s\tan dard\text{ deviation = }2.07 \end{gathered}]()