We have the function
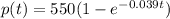
Therefore we want to determine when we have

It means that the term
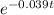
Must go to zero, then let's forget the rest of the function for a sec and focus only on this term
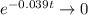
But for which value of t? When we have a decreasing exponential, it's interesting to input values that are multiples of the exponential coefficient, if we have 0.039 in the exponential, let's define that
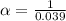
The inverse of the number, but why do that? look what happens when we do t = α
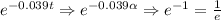
And when t = 2α
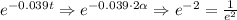
We can write it in terms of e only.
And we can find for which value of α we have a small value that satisfies
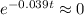
Only using powers of e
Let's write some inverse powers of e:
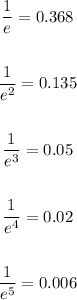
See that at t = 5α we have a small value already, then if we input p(5α) we can get

That's already very close to 550, if we want a better approximation we can use t = 8α, which will result in 549.81, which is basically 550.
Therefore, we can use t = 5α and say that 3 people are not important for our case, and say that it's basically 550, or use t = 8α and get a very close value.
In both cases, the decimal answers would be
