Given the following complex number
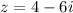
We will find the cube root of the complex number using the following formula:
![^3√(z)=\sqrt[3]z*(cos\text{ }(\theta+2\pi k)/(3)+i*sin\text{ }(\theta+2\pi k)/(3))](https://img.qammunity.org/2023/formulas/mathematics/college/sv6njyembkfmk2z3k927f2re1oane0ww8y.png)
The formula is called De Moivre's theorem of the nth root
We have substituted n = 3
So, first, we will convert the given number from the rectangular form to the polar form
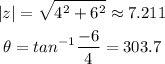
Substitute the magnitude and the angle and k = 0, 1, 2
So, there are 3 cubic roots of the given number as follows:
![\begin{gathered} k=0\rightarrow z_1=\sqrt[3]{7.211}(cos(303.7)/(3)+i*sin(303.7)/(3))=1.932(cos101.23+i*sin101.23) \\ \\ k=1\rightarrow z_2=\sqrt[3]{7.211}(cos(303.7+2\pi)/(3)+i*sin(303.7+2\pi)/(3))=1.932(cos221.23+i*sin221.23) \\ \\ k=2\rightarrow z_3=\sqrt[3]{7.211}(cos(303.7+4\pi)/(3)+i*sin(303.7+4\pi)/(3))=1.932(cos341.23+i*sin341.23) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sjh4txie6aq2wsddjiyjptxd9syao5a7ci.png)