Question

theres 2 fill in the blank boxes and 3 drop down menus, below i will list the options in the drop down menus.box 1 - apply quotient identities, apply Pythagorean identities, apply double-number identities, apply even-odd identities.box 2 - apply cofunction identities, use the definition of subtraction, apply even-odd identities, Write as one expresssion combine like terms.box 3 - apply cofunction identities, apply double-number identities, apply Pythagorean identities, apply even-odd identities.

Answer 1

Box 1 : Apply Quotient Identities

`cotx-tanx=(cosx)/(sinx)-(sinx)/(cosx)`

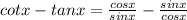
The answer for the first box is

`\begin{equation*} (cosx)/(sinx)-(sinx)/(cosx) \end{equation*}`

Box 2: Write as one expression

`\begin{gathered} cotx-tanx=(cosx)/(s\imaginaryI nx)-(s\imaginaryI nx)/(cosx) \\ cotx-tanx=(cosx(cosx)-sinx(sinx))/(sinxcosx) \\ cotx-tanx=(cos^2x-sin^2x)/(sinxcosx) \end{gathered}`

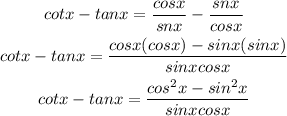
The answer for the second box is

`(cos^(2)x-s\imaginaryI n^(2)x)/(s\imaginaryI nxcosx)`

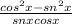
Before the box 3, please note the identity

Note: Trigonometry I dentities

`\begin{gathered} cos^2x-s\mathrm{i}n^2x=cos2x \\ 2sinxcosx=sin2x \end{gathered}`

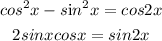
Box 3: Apply Double - Number Identities

`\begin{gathered} cotx-tanx=(cos^(2)x-s\imaginaryI n^(2)x)/(s\imaginaryI nxcosx) \\ Applying\text{ the above trigonometry identities} \\ cotx-tanx=(cos2x)/(sinxcosx) \\ cotx-tanx=(cos2x)/(sinxcosx)*(2)/(2) \\ cotx-tanx=(2cos2x)/(2sinxcosx) \\ cotx-tanx=(2cos2x)/(sin2x) \end{gathered}`