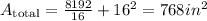Question

What is the minimum surface area that such a box can have

Answer 1

Given a rectangular box with an open top and square base, the dimensions of the box are:

`a* a* b`

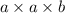
The volume can be calculated as:

`V=a\cdot a\cdot b=a^2\cdot b`

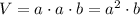
The area of the sides is:

`A_L=a\cdot b`

The area of the base:

`A_B=a^2`

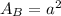
There are 4 lateral sides and 1 base (the top is open), so the total surface area is:

`A_{\text{total}}=4\cdot A_L+A_B=4\cdot a\cdot b+a^2`

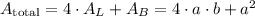
We have a fixed volume of 2048 in³, then:

`\begin{gathered} a^2\cdot b=2048 \\ b=(2048)/(a^2) \end{gathered}`

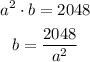
Using this result on A_total:

`A_{\text{total}}=4\cdot a\cdot(2048)/(a^2)+a^2=(8192)/(a)+a^2`

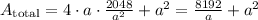
To find the minimum surface area, we take the derivative:

`\begin{gathered} (dA_(total))/(da)=-(8192)/(a^2)+2a=0 \\ a^3=4096 \\ a=16 \end{gathered}`

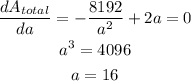
Now, we calculate the minimum total area using a:

`A_{\text{total}}=(8192)/(16)+16^2=768in^2`