Solution
Notice that we have two solid shapes and we want to find the surface area of the composite.
We have a triangular prism on a cuboid.
Note: Formula For Finding the Surface Area Of A Cuboid
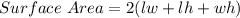
From the question, we have that
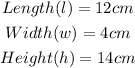
The area will be

Now, we find the Area of the Triangular Prism
Note: Formula To Use
From the question, we have
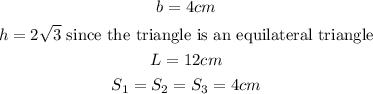
Substituting we have
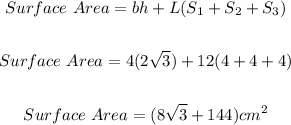
Therefore, the total surface area of the composite is
