McKenzie wants to determine which ice cream option is the best choice.
Part (a)
Volume of Scoop:
A scoop of ice cream is considered a perfect sphere and has a 2-inch diameter.
The volume of the sphere is given by
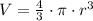
Where r is the radius.
We know that radius is half of the diameter.
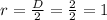
So, the volume of a scoop of ice cream is
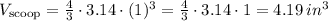
Therefore, the volume of a scoop of ice cream is 4.19 in³
Volume of Cone:
A cone has a 2-inch diameter and a height of 4.5 inches.
The volume of a cone is given by
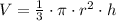
Where r is the radius and h is the height of the cone.
We know that radius is half of the diameter.
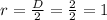
So, the volume of a cone of ice cream is
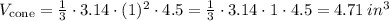
Therefore, the volume of a cone of ice cream is 4.71 in³
Volume of Cup:
A cup, considered a right circular cylinder, has a 3-inch diameter and a height of 2 inches.
The volume of a right circular cylinder is given by

Where r is the radius and h is the height of the right circular cylinder.
We know that radius is half of the diameter.
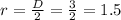
So, the volume of a cup of ice cream is
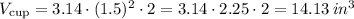
Therefore, the volume of a cup of ice cream is 14.13 in³
Part (b)
Now let us compare the various given options and decide which option is the best value for money
Option 1:
The price of one scoop in a cup is $2
The volume of one scoop of ice cream is 4.19 in³
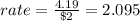
Option 2:
The price of two scoops in a cup is $3
The volume of one scoop of ice cream is 4.19 in³

Option 3:
The price of three scoops in a cup is $4
The volume of one scoop of ice cream is 4.19 in³
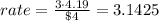
Option 4:
The price of half a scoop in a cone is $2
The volume of one scoop of ice cream is 4.19 in³
The volume of one cone of ice cream is 4.71 in³
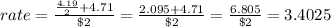
Option 5:
The price of a cup filled with ice cream is $4
The volume of a cup is 14.13 in³

As you can see, the option 5 (a cup filled with ice cream) has the highest rate (volume/$)
This means that option 5 provides the best value for money.
Therefore, McKenzie should choose "a cup filled with ice cream level to the top of cup" for the best value for money.