First, consider that the distance traveled by the car in 0.75s is:
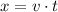
Convert 90km/h to m/s as follow:
![\frac{90\operatorname{km}}{h}\cdot(1h)/(3600)\cdot\frac{1000m}{1\operatorname{km}}=(25m)/(s)]()
Then, the distance x is:

Then, when the driver start to apply the brakes, the distance to the barrier is:
x' = 40.0 m - 18.75 m = 21.25 m
Next, calculate the distance that the car need to stop completely, by using the following formula:

where,
v: final velocity = 0m/s (the car stops)
vo: initial velocity = 25m/s
a: acceleration = 10m/s^2
d: distance = ?
Solve the previous equation for d and replace the values of the other parameters:
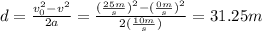
Then, the drive needs 31.25 m to stop. If you compare the previous result with the distance of the car related to the barrier when the driver applies the brakes
(x' = 18.75 m), you can notice that d is greater than x'.
Hence, the car does hit the barrier.