Question

24) The radius of a circle is 6 inches. What is the area of a sector that has a central angle of 100 degrees 

Answer 1

Area of the sector = 31.42 square inches

Step-by-step explanation

The area of a sector that has a central angle, θ, in a circle of radius r, is given as

`\begin{gathered} \text{Area of a sector = }(\theta)/(360\degree)*(Area\text{ of a circle)} \\ \text{Area of a circle =}\pi* r^2 \\ \text{Area of a sector = }(θ)/(360°)*\pi* r^2 \end{gathered}`

For this question,

θ = central angle = 100°

π = pi = 3.142

r = radius = 6 inches

`\begin{gathered} \text{Area of a sector = }(θ)/(360°)*\pi* r^2 \\ \text{Area of a sector = }(100\degree)/(360\degree)*3.142*6^2=31.42\text{ square inches} \end{gathered}`

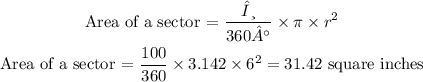
Hope this Helps!!!