Let's use the variable x to represent the second number. The first number is two fifths of x, so the first number is 2x/5.
If the sum of the numbers is 49, we can write the following equation:
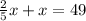
Now, solving the equation for x, we have:
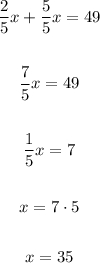
Let's calculate the first number:
![(2)/(5)x=(2)/(5)\operatorname{\cdot}35=2\cdot7=14]()
Therefore the numbers are 14 and 35.