Question

On average, people breath 10,000 times per night with a standard deviation of 1400. You study 50 people and record how many breaths they take per night. What is the probability that the average of all participants in the study was fewer than 10,200 breaths each night?I want answer with step by step.

Answer 1

`\begin{equation*} 0.84375 \end{equation*}`

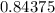
Step-by-step explanation

We want to find the probability that the average of all participants in the study was fewer than 10,200 breaths each night.

To do this, first, we have to find the z-score corresponding to the sample mean:

`z=(x-\mu)/((\sigma)/(√(n)))`

where x = sample mean

μ = population mean

σ = standard deviation

n = sample size

Therefore, the z-score is:

`\begin{gathered} z=(10200-10000)/((1400)/(√(50)))=(10200-10000)/((1400)/(7.0711)) \\ z=(200)/(197.99) \\ z=1.01 \end{gathered}`

Now, using the standard normal table, we can find P(z < 1.01).

Therefore, the probabilityis:

`P(z<1.01)=0.84375`

That is the answer.