Question

For the function f(x) = 6e^x, calculate the following function values:f(-3) = f(-1)=f(0)= f(1)= f(3)=

Answer 1

Consider the given function,

`f(x)=6e^x`

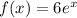
Solve for x=-3 as,

`\begin{gathered} f(-3)=6e^(-3) \\ f(-3)=6(0.049787) \\ f(-3)=0.2987 \end{gathered}`

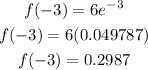
Thus, the value of f(-3) is 0.2987 approximately.

Solve for x=-1 as,

`\begin{gathered} f(-1)=6e^(-1) \\ f(-1)=6(0.367879) \\ f(-1)=2.2073 \end{gathered}`

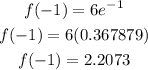
Thus, the value of f(-1) is 2.2073 approximately.

Solve for x=0 as,

`\begin{gathered} f(0)=6e^0 \\ f(0)=6(1) \\ f(0)=6 \end{gathered}`

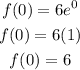
Thus, the value of f(0) is 6 .

Solve for x=1 as,

`\begin{gathered} f(1)=6e^1 \\ f(1)=6(2.71828) \\ f(1)=16.3097 \end{gathered}`

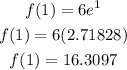
Thus, the value of f(1) is 16.3097 approximately.

Solve for x=3 as,

`\begin{gathered} f(3)=6e^3 \\ f(3)=6(20.0855) \\ f(3)=120.5132 \end{gathered}`

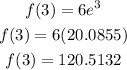
Thus, the value of f(3) is 120.5132 approximately.