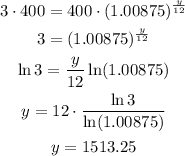Leah investment is:
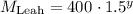
Where M is the ammount of money that she has, and y the number of years.
We want to know the number of years that must elapse for her investment to triple, so we want to know the value of y such that:
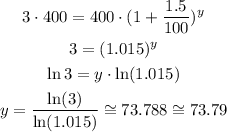
It will take 73.79 years to triple her investment.
Lauren investment is:
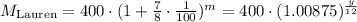
Where M is the ammount of money that she has, and m the number of months, and y is the number of years.
We want to know the number of years that must elapse for her investment to triple, so we want to know the value of y such that: