Question

3a. Sketch the line that goes through the points A(4,3) and B( 8, 1)Find the slope and the equation of line AB3b. Find the length of segment AB3c. Find the midpoint of segment AB

Answer 1

Hello! First, let's remember:

We can write a point as a cartesian coordinate (x, y).

The exercise has given two points, A(4,3) and B(8,1).

a. Slope:

To calculate the slope of a line, we can use the formula below:

`\text{Slope}=(y_2-y_1)/(x_2-x_1)`

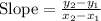
Let's consider A equal to the first point (4, 3) = (x1, y1), and B will be the second point (8, 1) = (x2, y2). Replacing these values in the formula:

`\text{Slope}=\frac{1_{}-(3)_{}}{8-(4)}=(-2)/(4)=-(1)/(2)`

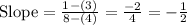
b. Lenght of segment AB:

To find this length, we have to use another formula. Now we will calculate the distance between two points:

`\text{Distance}=\sqrt[]{(x_2-x_1)^2+(y_2_{}-y_1_{})^2}`

Still considering A (4, 3) = (x1, y1), and B (8, 1) = (x2, y2), let's replace the values in the formula:

`\begin{gathered} \text{Distance}=\sqrt[]{(8_{}-4_{})^2+(1-3_{})^2} \\ \text{Distance}=\sqrt[]{(4_{})^2+(-2_{})^2} \\ \text{Distance}=\sqrt[]{(16^{}+4)^{}} \\ \text{Distance}=\sqrt[]{20} \\ \text{Distance}=2\sqrt[]{5} \end{gathered}`

c. Midpoint of segment AB:

This value will be the medium point. To calculate it, we'll use another formula:

`x_m=((x_1+x_2)/(2)+\frac{y_1+y_2_{}_{}}{2})`

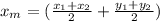
Still considering the same values for (x1, y1) and (x2, y2), let's replace them:

`\begin{gathered} x_m=(\frac{8+4_{}}{2},\frac{3+1_{}}{2}) \\ \\ x_m=(\frac{12_{}}{2},\frac{4_{}}{2}) \\ \\ x_m=(6,2) \end{gathered}`

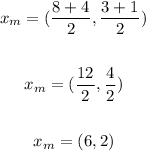
The midpoint of segment AB will be at point X (6, 2).

You can see this line represented in a cartesian plan below: