Question

In the picture shown below, a cube with a side of 5 inches is placed directly on top of a larger cube which has a side of 18 inches. Then, another cube with a side of 3 inches is placed directly to the side of the lower cube. What is the surface area of this assembly? (drawing below is not to scale)

Answer 1

For this problem, we are given three cubes. Cube A is on top of cube B, the cube C is glued to the side of cube B. We need to calculate the surface area for the whole piece.

The surface area of a cube is given by the following:

`A_{\text{surface}}=6\cdot l^2`

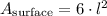
Where "l" is the measurement of the length of the side on each cube.

To calculate the whole surface area, we need to calculate each cube individually then sum them. Let's start with cube A, since this cube is on top of Cube b, one of its faces shouldn't count for the surface area, therefore we have:

`\begin{gathered} A_{\text{cubeA}}=5\cdot5^2=125\text{ square inches} \\ \end{gathered}`

Now we need to calculate the surface area for cube C, which is very similar to cube A, as shown below:

`A_{\text{cubeC}}=5\cdot3^2=45\text{ square inches}`

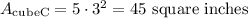
Finally, we need to calculate the area for cube B, this one is different because we need to subtract one face from cube A and one for group C.

`\begin{gathered} A_{\text{cubeB}}=6\cdot18^2-5^2-3^2 \\ A_{\text{cubeB}}=6\cdot324-25-9 \\ A_{\text{cubeB}}=1994-25-9=1910 \end{gathered}`

The total area is the sum of all areas:

`A=1910+45+125=2080`

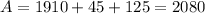
The total surface area is equal to 2080 square inches.