To solve the equation system by substitution, since the equations are expressed in terms of y, you have to equal both expressions and calculate the value of x:


To calculate the value of x, the first step is to pass the x-term to the left side of the equation by applying the opposite operation:
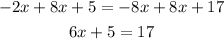
Next, pass 5 to the right side of the equation:

Finally, divide both sides by 6 to reach the value of x
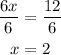
Now that we have determined the value of x, replace it in either one of the original equations to determine the value of y:
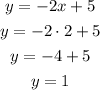
The solution for this equation system is (2,1)