Solution:
Given:
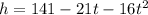
To get the time the ball hit the ground, it hits the ground when the height is zero.
Hence,
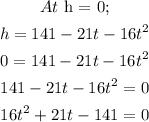
To solve for t, we use the quadratic formula.
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where;} \\ a=16,b=21,c=-141 \\ t=\frac{-21\pm\sqrt[]{21^2-(4*16*-141)}}{2*16} \\ t=\frac{-21\pm\sqrt[]{441+9024}}{32} \\ t=\frac{-21\pm\sqrt[]{9465}}{32} \\ t=(-21\pm97.288)/(32) \\ t_1=(-21+97.288)/(32)=(76.288)/(32)=2.384\approx2.38 \\ t_2=(-21-97.288)/(32)=(-118.288)/(32)=-3.6965\approx-3.70 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wydr8ogx9gutmfe4h446vec3uzs8ds4api.png)
Since time can't be a negative value, we pick the positive value of t.
Therefore, to the nearest hundredth, it takes 2.38 seconds for the ball to hit the ground.