We have to find the dimensions of a box with a volume that is at least 1000 cm³.
We have to find the dimensions that require the minimum amount of material.
We can draw the box as:
The volume can be expressed as:
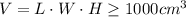
The material will be the sum of the areas:
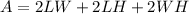
Since the box is square-based, the width and length are equal and we can write:
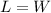
Then, we can re-write the area as:

Now, we have the area expressed in function of L and H.
We can use the volume equation to express the height H in function of L:
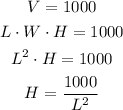
We replace H in the expression for the area:
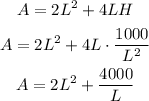
We can now optimize the area by differentiating A and then equal the result to 0:
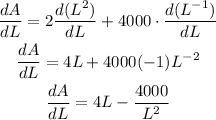
![\begin{gathered} (dA)/(dL)=0 \\ 4L-(4000)/(L^2)=0 \\ 4L=(4000)/(L^2) \\ L\cdot L^2=(4000)/(4) \\ L^3=1000 \\ L=\sqrt[3]{1000} \\ L=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zsrl37ha2t1r4fbyqro4f4sgi83ohglm5c.png)
We now can calculate the other dimensions as:
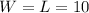
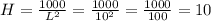
Then, the dimensions that minimize the surface area for a fixed volume of 1000 cm³ is the length, width and height of 10 cm, which correspond to a cube (all 3 dimensions are the same).
Answer: the dimensions are length = 10 cm, width = 10 cm and height = 10 cm.