Question

identify the amplitude and period of the function then graph the function and describe the graph of G as a transformation of the graph of its parent function

Answer 1

Given the function:

`g(x)=cos4x`

Let's find the amplitude and period of the function.

Apply the general cosine function:

`f(x)=Acos(bx+c)+d`

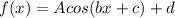
Where A is the amplitude.

Comparing both functions, we have:

A = 1

b = 4

Hence, we have:

Amplitude, A = 1

To find the period, we have:

`(2\pi)/(b)=(2\pi)/(4)=(\pi)/(2)`

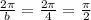
Therefore, the period is = π/2

The graph of the function is shown below:

The parent function of the given function is:

`f(x)=cosx`

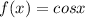
Let's describe the transformation..

Apply the transformation rules for function.

We have:

The transformation that occured from f(x) = cosx to g(x) = cos4x using the rules of transformation can be said to be a horizontal compression.

ANSWER:

Amplitude = 1

Period = π/2

Transformation = horizontal compression.