Answer:
Parallelogram. Option A is correct
Explanations:
In order to determine the best name for a quadrilateral with the given vertices, we will find the measure of the distance AB, BC, CD, and AD using the distance formula as shown;
![D=\sqrt[]{(x_2-x_1)^2+(y_2-y^{}_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/nyc5crhshukmro115tkfjgfpno82kjnu65.png)
For the measure of AB with coordinates A(5,-2), B(2,2);
![\begin{gathered} AB=\sqrt[]{(5-2)^2+(-2-2^{}_{})^2} \\ AB=\sqrt[]{3^2+(-4)^2} \\ AB=\sqrt[]{9+16} \\ AB=\sqrt[]{25} \\ AB=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bt4xanwsaobfaym3gv5ahw577qzixcd5uo.png)
For the measure of BC with coordinates B(2,2) and C(1, -5)
![\begin{gathered} BC=\sqrt[]{(2-1)^2+(2-(-5^{}_{}))^2} \\ BC=\sqrt[]{1^2+7^2} \\ BC=\sqrt[]{50} \\ BC=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gk1mnuoyt1ba5cct46jtt2bgbszgtu6937.png)
For the measure of CD with coordinates C(1,-5), and D(-2,-1);
![\begin{gathered} CD=\sqrt[]{(1-(-2))^2+(-5-(-1^{}_{}))^2} \\ CD=\sqrt[]{3^2+(-4)^2} \\ CD=\sqrt[]{9+16} \\ CD=\sqrt[]{25} \\ CD=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t7rthqnojmo0x812o53gnmk1ttk4yawt8q.png)
For the measure of AD with coordinates A(5, -2), and D(-2,-1);
![\begin{gathered} AD=\sqrt[]{(5-(-2))^2+(-2-(-1^{}_{}))^2} \\ AD=\sqrt[]{(5+2)^2+(-2+1)^2} \\ AD=\sqrt[]{7^2+(-1)^2} \\ AD=\sqrt[]{50} \\ AD=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fwh51y54w9d9qn5kd45goz0l0gdy80rrwl.png)
For the slopes;
Check if the length AB is perpendicular to AD
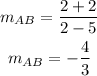
For the slope of AD
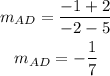
Since AB is not perpendicular to AD, hence the quadrilateral is not a rectangle and also not a square or rhombus since all the sides are not equal.
From the given distances, you can see that opposite sides are equal (AB = CD and BC = AD ), hence the best name for a quadrilateral is a parallelogram.