Firstly, let us define natural numbers.
Natural numbers are simply positive intergers, that is integers that are greater than zero e.g 1,2,3,4...
Secondly, when is a set said to be closed under a particular operation?
A set is said to be closed under an operation if and only if the operation on any two elements of the set produces another element of the same set. for example when you perform an operation (like addition) on a set of number (like natural numbers) it must give you a number from that same set.
E.g
let's check whether natural numbers are closed under the operation of adddition.
taking two numbers 3 and 5.

since the operation gives us 8, which is a natural number, it means natural numbers are closed under the operation of addition.
Back to the main question, which is to check whether natural numbers are closed under the operation of subtraction.
taking two cases.
case 1; taking numbers 3 and 5
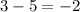
case 2: taking numbers 7 and 2
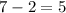
From the two cases, case 2 gave us a natural number while case 1 does not give us a natural number.
This means that Natural numbers are not Closed under subtraction.
Because subtraction operation on natural numbers does not necessarily produce another natural number.
On a general note;
Natural numbers are closed under Addition and Multiplication operations
while They are not closed under subtraction and division operation