Question

How do I tell if a parabola has a minimum or a maximum?

Answer 1

We can write the equation of a parabola in two different ways:

The standard form:

`\begin{gathered} y=ax^2+bx+c \\ a\\e0 \end{gathered}`

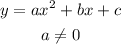
And the vertex form:

`y=a(x-h)^2+k`

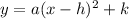
If the parabola has a minimum or a maximum depends on the leading coefficient (the coefficient of x²) or in both cases the coefficient a.

Let's see the cases:

`a>0_{\text{ }}(a_{\text{ }}is_{\text{ }}positive)`

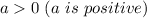
If a is positive, the parabola opens upwards, so the parabola has a minimum.

`a<0_{\text{ }}(a_{\text{ }}is_{\text{ }}negative)`

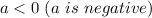
If a is negative, the parabola opens downwards, so the parabola has a maximum