The problem says you have 10 books arranged on a shelf and then you are choosing 4 books in alphabetical order.
Given that you are choosing books with an order (alphabetical) it means the order does matter, then it is a permutation (which is an ordered combination).
In this case, no repetitions are allowed because you can't repeat a book in the selection, they'll be 4 different books from the shelf, the formula you have to use is:
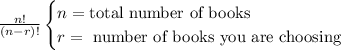
Then n=10 and r=4, replace these values:
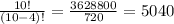
Then, can be chosen 5040 different groups of books.
The answer is option D.