To answer this question, we have that, if two triangles are similar, they maintain the same proportion on their corresponding sides.
We have that the corresponding sides are QP and TS, OP and RS, and QO and TR, so we can write:
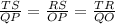
Then, since we have the values for QP, TS, and OP, we can find RS using the above proportion:

Then, we have that we can round this value to 30.11 units, and if we round the answer to the nearest tenth, we finally have that RS = 30.1 units.