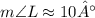Question

Find the measure of angle L. Round youranswer to the nearest degree.

Answer 1

Given the triangle KLM, you can find the measure of angle L by using the Law of Sines. This states that:

`(sinA)/(a)=(sinB)/(b)=(sinC)/(c)`

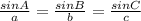
Where "a", "b" and "c" are sides of the triangle, and "A", "B", and "C" are the angles.

In this case, you can set up this equation:

`(sinK)/(k)=(sinL)/(l)`

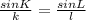
Knowing that:

`\begin{gathered} m\angle K=22\text{\degree} \\ k=56 \\ l=26 \end{gathered}`

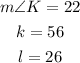
You can substitute values into the equation and solve for "L". Remember the use the Inverse Trigonometric Function Arcsine, in order to solve for the angle:

`(sin(22°))/(56)=(sinL)/(26)`
`(26\cdot sin(22°))/(56)=sinL`
`sin^(-1)((26\cdot sin(22°))/(56))=L`
`m\angle L\approx10°`

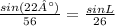
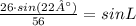
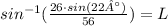
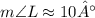
Hence, the answer is:

`m\angle L\approx10°`