1.
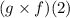
It means multiply f(x) and g(x) and then put "2" into it. The solution is what we are looking for. So,
![\begin{gathered} (g* f)(2)=\sqrt[]{11-4x}*1-x^2 \\ =\sqrt[]{11-4(2)}*1-(2)^2 \\ =\sqrt[]{3}*-3 \\ =-3\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9exdzxra6fdn6ycyabagrmk65886yzqrue.png)
2.
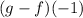
For this we subtract f from g and put -1 into the expression. So
![\begin{gathered} (g-f)(-1)=\sqrt[]{11-4x}-1+x^2 \\ =\sqrt[]{11-4(-1)}-1+(-1)^2 \\ =\sqrt[]{15}-1+1 \\ =\sqrt[]{15} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gf2vd0odrxuk1mws2l6e8et412opwlg7x8.png)
3.
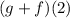
We simply add f and g and put 2 into the final expression.
![\begin{gathered} (g+f)(2)=\sqrt[]{11-4x}+1-x^2 \\ =\sqrt[]{11-4(2)}+1-(2)^2 \\ =\sqrt[]{3}-3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1p596tkclymo69nhgpoqlmkutgd2qlgp3r.png)
4.

We divide f by g and put -1 in the final expression. Shown below:
![\begin{gathered} ((f)/(g))(-1)=\frac{1-x^2}{\sqrt[]{11-4x}} \\ =\frac{1-(-1)^2}{\sqrt[]{11-4(-1)}} \\ =\frac{0}{\sqrt[]{15}} \\ =0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3k795u96bju8w79faparfjbyq0z91g0t3w.png)
Now, please match each answer with each choice.