Question

I have question 3 and need to know a b and c

Answer 1

a) Recall that:

`-1\le\cos \theta\le1.`

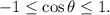
Therefore:

`\begin{gathered} -1\le\cos (30^(\circ)* t)\le1, \\ -12\le12\cos (30^(\circ)* t)\le12, \\ -12+16\le12\cos (30^(\circ)* t)+16\le12+16, \\ 4\le12\cos (30^(\circ)* t)+16\le28. \end{gathered}`

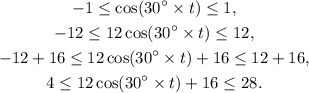
Therefore the minimum height of the Ferris wheel above the ground is 4 meters.

b) Recall that to evaluate a function at a given value, we substitute the variable by the given value, then, evaluating the given function at t=3 we get:

`12\cos (30^(\circ)*3)+16.`

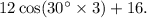
Simplifying the above result we get:

`\begin{gathered} 12\cos (90^(\circ))+16, \\ 12\cdot0+16, \\ 0+16, \\ 16. \end{gathered}`

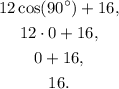
Therefore, the height of the Ferris wheel above the ground after 3 minutes is 16 meters.

(c) Let x be the time in minutes the Ferris wheel takes to complete one full rotation, then we can set the following equation:

`30^(\circ)* x=360^(\circ).`

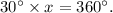
Therefore:

`30x=360.`

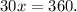
Dividing the above equation by 30 we get:

`\begin{gathered} (30x)/(30)=(360)/(30), \\ x=12. \end{gathered}`

Answer:

(a) 4 meters.

(b) 16 meters.

(c) 12 minutes.