1 Answer

Marine Le Borgne · Answer 1 · 2023-12-14T02:16:51+0000

Step-by-step explanation:

This figure is a rectangle and a quarter of a circle. We can find their areas and add them to find the total area of the figure.

The area of the rectangle is:

$A_{\text{rectangle}}=17cm*10\operatorname{cm}=170\operatorname{cm}^2$

The area of a circle is:

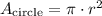
$A_{\text{circle}}=\pi\cdot r^2$

Where r is the radius of the circle. In this case we have a quarter of a circle, so its area is a quarter of the area of the circle:

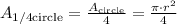
$A_{1/4\text{circle}}=\frac{A_{\text{circle}}}{4}=(\pi\cdot r^2)/(4)$

The radius of this circle is 8cm:

$A_{1/4\text{circle}}=(\pi\cdot8^2)/(4)=(\pi\cdot64)/(4)=\pi\cdot16\approx50.27\operatorname{cm}^2$

The total area of the figure is:

$A_{\text{figure}}=A_{\text{rectangle}}+A_{1/4\text{circle}}=170\operatorname{cm}+50.27\operatorname{cm}=220.27\operatorname{cm}^2$

Answer:

The area is 220.27 cm²

Please log in or register to add a comment.