Answer:
379,001.
Step-by-step explanation:
The population of the city grows by 4.25%.
This is a constant factor and models an exponential function.
An exponential population function is of the form:

From the given problem:

This then gives us:
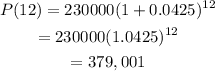
The population after 12 years will be approximately 379,001.