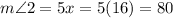Question

In the figure, m < 1= (x-6)º and m2 2= (5x).

Answer 1

We have the measure of angles 1 and angle 2, as we can see from the diagram in the image, angles 1 and 2 added form the right angle (90°) in the figure.

Thus, the sum of x-6 and 5x, must be equal to 90°.

(a) Write an equation:

`x-6+5x=90`

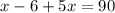
(b) To find the degree measure of each angle, first we need to solve for the value of x in the equation.

Combining like terms:

`6x-6=90`

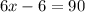
Adding 6 from both sides:

`\begin{gathered} 6x-6+6=90+6 \\ 6x=96 \\ \end{gathered}`

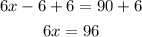
Divide both sides by 6:

`\begin{gathered} (6x)/(6)=(96)/(6) \\ x=16 \end{gathered}`

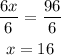
Now that we have x, we find angle 1:

`m\angle1=x-6=16-6=10`

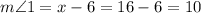
And the measure of angle 2:

`m\angle2=5x=5(16)=80`