Step 1
Given;
For an outdoor concert by the city orchestra, concert organizers estimate that 11,000 people will attend if it's not raining.
If it is raining, concert organizers estimate 7000 people will attend.
On the day of the concert, meteorologists predict a 60% chance of rain.
Step 2
Given that the probability of having rain is 60%
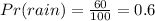
So the probability of not having rain is;
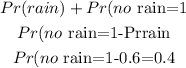
Step 3
Now, the expected number of people who will attend the concert will be:
=(probability of not having rain x number of expected guests when it does not rain) + (probability of having rain x number of expected guests when rains)
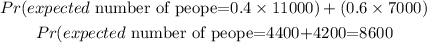
Answer; So, the expected number of people who will attend the concert is 8600