Conditional Probability
First, we must complete the totals in the table as follows:
The formula for the conditional probability is:
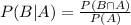
Where A is an event we know has already occurred, B is an event we want to calculate its probability of occurrence, and P∩A is the probability of both occurring.
We know a female student has been selected, so that is our known event and:
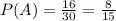
The probability that a female student is also a senior is:
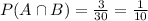
Substituting:
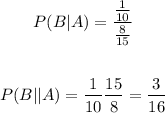
The required probability is 3/16