Question

May I please get help with this math problem it’s so confusing

Answer 1

We have to find the value of z and x.

We assume that lines g and h are parallel.

Then, z and the angle with measure 85° are consecutive interior angles.

As they are conscutive interior angles, their measures add 180°.

Then, we can write:

`\begin{gathered} z+85\degree=180\degree \\ z=180-85 \\ z=95\degree \end{gathered}`

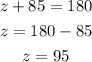
Then, we can relate the angle with measure z with the angle with measure (6x-109). They are vertical angles and, therefore, they have the same measure.

Then, we can write:

`\begin{gathered} z=6x-109 \\ 95=6x-109 \\ 95+109=6x \\ 204=6x \\ x=(204)/(6) \\ x=34 \end{gathered}`

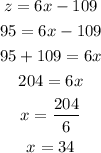
Answer: z = 95 and x = 34.