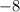Question

Half of the smaller of two consecutive even integers is equal to two more than the larger integer find the smaller even integer

Answer 1

Let the first even integer be 'a'.

Let the second integer be (a + 2) since the second is a consecutive even integer.

Half of the smaller (i.e. a) is equal to two more than the larger (i.e. a + 2). In other words:

`(a)/(2)=(a+2)+2`

Evaluate for a

Simplify

`\begin{gathered} (a)/(2)=a+2+2 \\ (a)/(2)=a+4 \end{gathered}`

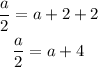
Multiply all through by 2

`\begin{gathered} 2*(a)/(2)=2* a+2*4 \\ a=2a+8 \end{gathered}`

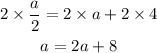
Collect like terms

`\begin{gathered} -8=2a-a \\ -8=a \\ \therefore a=-8 \end{gathered}`

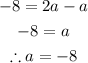
Hence, the smaller even integer is

`-8`