Question

In the diagram segment AD and AB are tangent to circle C solve for x

Answer 1

A property ostates that if two lines that are tangent to the circle intersect in an external point, they are congruent, i.e. they have the same length.

`\begin{gathered} AD=AB \\ x^2+2=11 \end{gathered}`

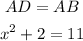
From this expression we can determine the possible values of x. The first step is to equal the expression to zero

`\begin{gathered} x^2+2-11=11-11 \\ x^2+2-11=0 \\ x^2-9 \end{gathered}`

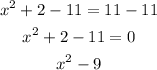
The expression obtained is a quadratic equation, using the queadratic formula we can determine the possible values of x:

`\begin{gathered} f(x)=ax^2+bx+c \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

For our expression

`x^2+0x+-9`

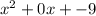
The coefficients are

a=1

b=0

c=-9

Replace them in the formula

`\begin{gathered} x=\frac{-0\pm\sqrt[]{0^2-4\cdot1\cdot(-9)}}{2\cdot1} \\ x=\frac{0\pm\sqrt[]{36}}{2} \\ x=(0\pm6)/(2) \end{gathered}`

Now calculate both possible values:

Positive:

`\begin{gathered} x=(+6)/(2) \\ x=3 \end{gathered}`

Negative:

`\begin{gathered} x=(-6)/(2) \\ x=-3 \end{gathered}`

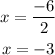
The possible values of x are 3 and -3