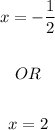Question

Kiran is solving 2x-3/x-1=2/x(x-1) for x, and he uses these steps.He checks his answer and finds that it isn’t a solution to the original equation, so he writes “no solutions.” Unfortunately, Kiran made a mistake while solving. Find his error and calculate the actual solution(s).

Answer 1

Given:

`\begin{gathered} To\text{ solve,} \\ (2x-3)/(x-1)=(2)/(x(x-1)) \end{gathered}`

Kiran multiplied the left-hand side of the equation by (x-1) and multiplied the right-hand side of the equation by x(x-1).

That was where he made the mistake. He ought to have multiplied both sides with the same quantity (Lowest Common Denominator) so as not to change the actual value of the question.

Multiplying both sides by the same quantity does not change the real magnitude of the question.

The actual solution goes thus,

`\begin{gathered} (2x-3)/(x-1)=(2)/(x(x-1)) \\ \text{Multiplying both sides of the equation by the LCD,} \\ \text{The LCD is x(x-1)} \\ x(x-1)((2x-3)/(x-1))=x(x-1)((2)/(x(x-1))) \\ x(2x-3)=2 \\ \text{Expanding the bracket,} \\ 2x^2-3x=2 \\ \text{Collecting all the terms to one side to make it a quadratic equation,} \\ 2x^2-3x-2=0 \end{gathered}`

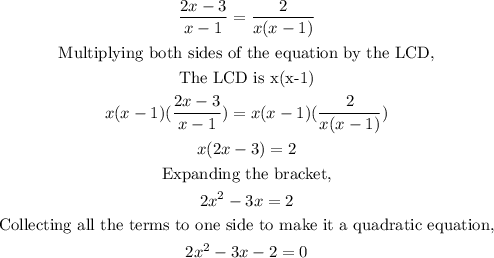
Solving the quadratic equation;

`\begin{gathered} 2x^2-3x-2=0 \\ 2x^2-4x+x-2=0 \\ \text{Factorizing the equation,} \\ 2x(x-2)+1(x-2)=0 \\ (2x+1)(x-2)=0 \\ 2x+1=0 \\ 2x=0-1 \\ 2x=-1 \\ \text{Dividing both sides by 2,} \\ x=-(1)/(2) \\ \\ \\ OR \\ x-2=0 \\ x=0+2 \\ x=2 \end{gathered}`

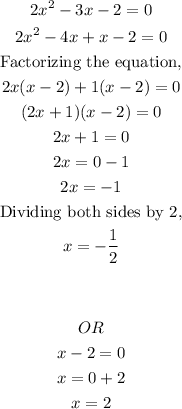
Therefore, the actual solutions to the expression are;

`\begin{gathered} x=-(1)/(2) \\ \\ OR \\ \\ x=2 \end{gathered}`