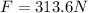Question

You want to lift a heavy box with a mass L = 64.0 kg using the two-ideal pulley system as shown. With what minimum force do you have to pull down on the rope in order to lift the box at a constant velocity? One pulley is attached to the ceiling and one to the box.

Answer 1

The given problem can be solved using the following free-body diagram:

The diagram is the free-body diagram for the pulley that is holding the weight. Where:

`\begin{gathered} T=\text{ tension} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \end{gathered}`

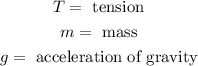
Now we add the forces in the vertical direction:

`\Sigma F_v=T+T-mg`

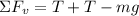
Adding like terms:

`\Sigma F_v=2T-mg`

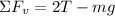
Now, since the velocity is constant this means that the acceleration is zero and therefore the sum of forces is zero:

`2T-mg=0`

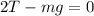
Now we solve for "T" by adding "mg" from both sides:

`2T=mg`

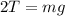
Now we divide both sides by 2:

`T=(mg)/(2)`

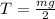
Now we substitute the values and we get:

Solving the operations:

`T=313.6N`

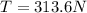
Now we use the free body diagram for the second pulley:

Now we add the forces in the vertical direction:

`\Sigma F_v=T-F`

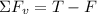
The forces add up to zero because the velocity is constant and the acceleration is zero:

`T-F=0`

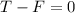
Solving for the force:

`T=F`

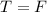
Therefore, the pulling force is equal to the tension we determined previously and therefore is:

`F=313.6N`