Given,
System of equation is,

Taking the equation (i) as,
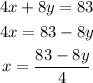
Substituting the value of x in equation (ii) then,
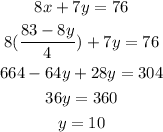
Substituting the value of y in above equation then,
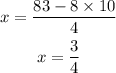
Hence, the value of x is 3/4 and y is 10. (3/4, 10)
System of equation is,

Taking the equation (i) as,
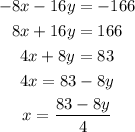
Substituting the value of x in equation (ii) then,
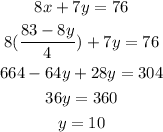
Substituting the value of y in above equation then,
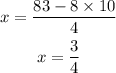
Hence, the value of x is 3/4 and y is 10. (3/4, 10)