Question

Y = 17x - 8, y = 24x +6 Parallel Perpendicular Neither

Answer 1

Two parallel lines in the coordinate system share the same slope, this means that if you have two parallel lines:

`\begin{gathered} y_1=m_1x_1+b_1 \\ y_2=m_2x_2+b_2 \\ \text{Their slopes must be equal:} \\ m_1=m_2 \end{gathered}`

For the given equations, the slopes are:

`\begin{gathered} y=17x-8 \\ m=17 \end{gathered}`
`\begin{gathered} y=24x+6 \\ m=24 \end{gathered}`

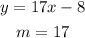
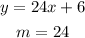
The slopes are different, so this lines are not parallel.

Two lines are perpendicular, when the slope of one of them is the negative inverse of the first one, this is for the perpendicular lines:

`\begin{gathered} y_1=m_1x_1+b_1 \\ y_2=m_2x_2+b_2 \\ m_2=-(1)/(m_1) \end{gathered}`

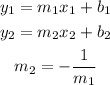
For the given equations, using y=17x-8 as reference, the slope of a line perpendicular to this one must be:

`m_{}=-(1)/(17)`

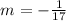
The slope of a perpendicular line to y=17x-8 is different from the slope of the second given line, so you can conclude that these lines are not perpendicular.

The correct choice is Neither